With this article you’ll begin your journey with the Scheme programming language by first learning how to read and understand expressions and then how to write them. When you reach the end of this article you’ll be ready to group your expressions into larger components such as functions.
It will be most helpful if you follow along with the article using one of the free Scheme interpreters such as Chicken Scheme or Racket. Both are easy to install and support all the popular operating systems (Windows, Mac, and Linux). If you don’t have a preference I recommend you download the Chicken Scheme installer.
Building programs from smaller pieces
Expressions are the fundamental building blocks of a programming language. As a programmer you’ll spend a great deal of your time combining expressions together in order to build larger components that eventually make up an entire application just like when you create buildings from small toy bricks.
Usually, however, programmers will spend some time thinking about the application they are going to write and how it should fit together as a whole before they start dealing with the smaller details like expressions, this is called top-down design. This article series uses the opposite approach to teach programming, namely bottom-up.
Using a bottom-up approach we’ll start with the smaller components (i.e. expressions) and work our way up to more complicated programming structures. For now I just want you to be aware that taking an idea for a big application and jumping directly to writing expressions in a programming language without first thinking about how things fit together might be a recipe for trouble.
Breaking apart a simple Scheme expression
Let’s start with the example code from the previous article which added two numbers together. I’ll continue to use simple arithmetic throughout this article since it gives us common ground to start from, but you should keep in mind that expressions in Scheme can do more than just simple mathematical operations.
(+ 2 3)
In Scheme an expression is actually a list of items, much like a grocery list or a to-do list. A list in Scheme begins with an opening parenthesis, ends with a closing parenthesis, and in between contains one or more items separated from one another with whitespace. In the list above there are 3 items (often referred to as elements or members):
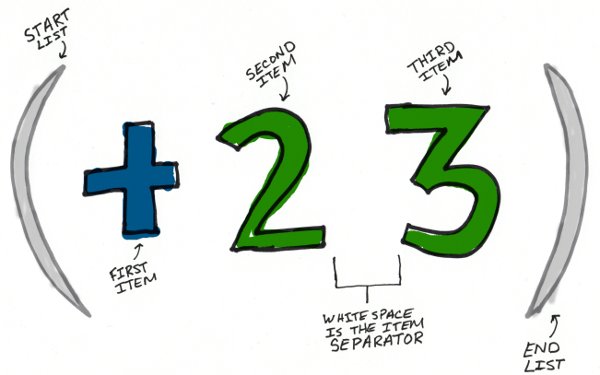
There’s not much more to it than that. Pretty simple right?
Evaluating simple expressions
An expression is pretty useless just sitting there on your screen
unless you actually make it do something. Making an expression
perform its task is called evaluation. Let’s evaluate this expression
in a Scheme interpreter. If you’re a good student you installed
Chicken Scheme as instructed at the beginning of the article. Open a
terminal window and run the csi tool. You should see the #;1>
prompt which means csi is waiting for you to enter an expression.
Type in our example expression from above (don’t forget the
parentheses) and then press enter/return. The csi tool should
evaluate the expression and print out the result (5), after which it
will return you to a new prompt and wait for your next expression.
When expressions are evaluated they will either return a result, produce a side effect (e.g. draw a rainbow), or both. Even though drawing rainbows is fun we’ll focus on expressions that return a result like our example expression that takes some numbers and returns their sum. Let’s break apart how our expression is evaluated.
Do you remember that an expression in Scheme is a list of items? The first item in the list (known as the head of the list, or more technically, the “car” of the list) is special. When the expression is being evaluated the interpreter begins by looking at the first item of the list which should be the name of a function. We’ll get into functions in the next article but for now you can think of a function as a task that you can ask Scheme to execute for you.
With the example expression we’ve been working with so far, the first
item of the list is +, the name of the function that adds
numbers. The remaining items of the list (known as the tail of the
list, or more technically the “cdr” of the list) are given to the +
function as arguments, in this case the numbers you want to add
together.
Arguments are the inputs to the function. Each function defines what
it wants for arguments (and some don’t want any). If you read the
documentation for the + function you’d find that it wants one or
more numbers as its arguments. Most programming languages come with a
set of predefined functions and allow you to define your own. Again,
we’ll get to that in the next article.
After an expression is evaluated it is replaced with its result. Don’t worry if that doesn’t make sense just yet, it will become clear in the next section when we start to put expressions together to form more complicated building blocks.
Combining expressions to form complex expressions
To spice things up a bit, pretend you’re a school teacher faced with grading a rather large stack of homework sheets. Your student aid already marked the incorrect answers but she didn’t calculate the percentages that the students are expecting to see.
Let’s write a Scheme expression to calculate the score for the first student’s worksheet. There are a total of 15 questions and the first student correctly answered 12. The arithmetic is pretty simple, divide 12 by 15 and multiple the result by 100:
(* 100 (/ 12 15))
Don’t panic, let’s work through this expression step by step.
First look at the parentheses, do you see that there are two lists in
the code above? The second list is inside the first, that is to say
one is nested inside the other. Both lists begin with the name of a
function (* is the name of a function that multiples its arguments
and / is the name of the function that divides its first argument by
its second argument).
When evaluating compound expressions like the one above the
interpreter will first evaluate the inner-most expression. In our
case that’s the expression that does the division. If you evaluate
the inner expression in csi you’ll find that the result is 0.8
(12/15 = 0.8).
Once you have the result of the inner expression you can replace it with its resulting value:
(* 100 0.8)
Now you’re left with a single expression and we already know how to evaluate those.
Unfortunately the only thing we’ve managed to do is turn Scheme into a boring calculator and haven’t really made grading papers any easier. Come to think of it, we’ve actually made it harder to grade papers because we have to hand type these weird nested Scheme expressions, repeating two of the numbers for each worksheet we grade.
Not to worry though, we’ll improve this quite a bit in the next article. The important thing is that you’ve learned about expressions and how to put them together to accomplish more complicated tasks.
List items, atoms, and constants
Before we wrap up let’s take a closer look at those things I’ve been calling list items. Did you notice from the code above that lists can contain other lists? Technically speaking lists are made up of atoms and/or other lists. An atom is anything that is not a list, so all the numbers and function names we’ve been using as list items are considered atoms.
More specifically, the numbers are called numeric constants because they can’t change (they are said to be hard-coded). Besides being constant values, numbers and text that are hard-coded are also referred to as literals.
While literal values in your code are useful there’s another way to get values into a running program, things called variables. With variables you essentially have a placeholder that you’ll fill in later when your program is running. Variables can be given values by asking the user a question, reading the current time from the computer’s clock, communicating with another computer, etc.
Scheme (like most programming languages) has support for different
types of values. We’ve already seen numbers and identifiers (e.g. +
and *). Using the following table, experiment with the Scheme
interpreter you installed. You can type the examples directly into
something like csi and it should give you back the value you
entered.
| Type | Description | Literal Examples |
|---|---|---|
| Integer | Whole numbers | -1, 0, and 5 |
| Real | Fractional numbers | 10.1 and 0.8 |
| Character | A single textual character | #\a, #\b, and #\c (the first 3 letters of the English alphabet) |
| String | A sequence of characters | "Hello World!" |
| Boolean | True and False | #t is true, #f is false |
| List | A list of values | '(1 2 3) |
There are a few other types of values that Scheme supports but we won’t be getting into those just yet. With the list of types above you can write complex and expressive programs. And don’t worry too much about literals, types, and variables right now. With more practice and through this series you’ll develop an intuition for using them.
Programs and values go hand in hand. From an abstract point of view programs are things that take some input values, translate those values, and then produce some sort of output based on those translated values.
Conclusion and next steps
In Scheme expressions are represented as lists that are delimited by parentheses and the items of the list are separated using whitespace. The first item in the list is the name of a function to execute and the remaining items are the arguments to that function.
When you nest an expression inside another expression the inner expression needs to be evaluated before the outer. You can think about evaluation as the act of replacing an expression with its resulting value.
In the next article we’ll look at how to group a set of expressions together to form a larger building block, a function. For now I’ll leave you with a teaser of what we’ll be working on next.
(define grade
(lambda (correct total)
(* 100 (/ correct total))))
(grade 12 15)
If you’re interested in following this series of articles I recommend that you subscribe to the RSS feed or keep an eye on the Learn to Program section of this site.